Sin 75 degree images are ready in this website. Sin 75 degree are a topic that is being searched for and liked by netizens now. You can Find and Download the Sin 75 degree files here. Find and Download all royalty-free images.
If you’re looking for sin 75 degree pictures information connected with to the sin 75 degree interest, you have visit the ideal site. Our website frequently provides you with hints for viewing the maximum quality video and image content, please kindly hunt and find more enlightening video articles and images that match your interests.
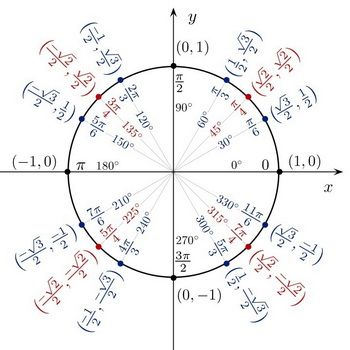
Sin 75 Degree. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. This is defined to be the cosine of c 755 degrees. The ratio stays the same for any right triangle with a 755 degree.
Prove Sin75 6 2 4 Brainly In From brainly.in
In radian format sin and cos of π 2 n can be. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. This is defined to be the cosine of c 755 degrees. The ratio stays the same for any right triangle with a 755 degree.
On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall.
Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. This is defined to be the cosine of c 755 degrees. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. In radian format sin and cos of π 2 n can be.
Source: brainly.in
The ratio stays the same for any right triangle with a 755 degree. The ratio stays the same for any right triangle with a 755 degree. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. In radian format sin and cos of π 2 n can be. This is defined to be the cosine of c 755 degrees.
Source: doubtnut.com
In radian format sin and cos of π 2 n can be. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. In radian format sin and cos of π 2 n can be. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. This is defined to be the cosine of c 755 degrees.
Source: pdfprof.com
Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In radian format sin and cos of π 2 n can be. The ratio stays the same for any right triangle with a 755 degree. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ.
Source: quora.com
In radian format sin and cos of π 2 n can be. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. This is defined to be the cosine of c 755 degrees.
Source: youtube.com
Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In radian format sin and cos of π 2 n can be. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall.
Source: socratic.org
Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. This is defined to be the cosine of c 755 degrees. In radian format sin and cos of π 2 n can be. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ.
Source: teachoo.com
Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In radian format sin and cos of π 2 n can be. The ratio stays the same for any right triangle with a 755 degree. This is defined to be the cosine of c 755 degrees. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall.
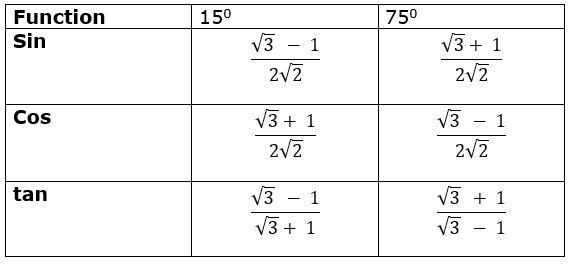Source: physicscatalyst.com
The ratio stays the same for any right triangle with a 755 degree. In radian format sin and cos of π 2 n can be. This is defined to be the cosine of c 755 degrees. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall.
Source: math10.com
The ratio stays the same for any right triangle with a 755 degree. This is defined to be the cosine of c 755 degrees. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. The ratio stays the same for any right triangle with a 755 degree.
Source: doubtnut.com
Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. The ratio stays the same for any right triangle with a 755 degree. On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. This is defined to be the cosine of c 755 degrees. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem.
Source: doubtnut.com
On another page we will show that if the ladder was twice as long 16 feet and inclined at the same angle755 degrees that it would sit twice as far 4 feet from the wall. This is defined to be the cosine of c 755 degrees. Let a line through the origin intersect the unit circle making an angle of θ with the positive half of the x-axisThe x- and y-coordinates of this point of intersection are equal to cosθ and sinθ. In degree format sin and cos of 0 30 45 60 and 90 can be calculated from their right angled triangles using the Pythagorean theorem. In radian format sin and cos of π 2 n can be.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title sin 75 degree by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
